Exercise 8.4
1. ABC is a triangle. D is a point on AB such that AD = 1/4 AB and E is a point on AC such that AE = 1/4 AC. If DE = 2 cm find BC.
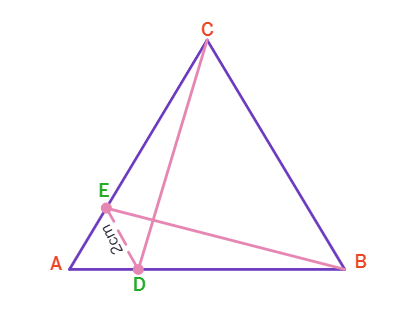
Solution:
Given:
AD =
AE =
DE =
To Find BC:
Proof:
∠A is common to both triangles ADE and ABC.
By
Therefore, DE/BC = AD/AB =
DE =
BC = 2 ×
Therefore, BC = 8 cm.
2. ABCD is quadrilateral E, F, G and H are the midpoints of AB, BC, CD and DA respectively. Prove that EFGH is a parallelogram.
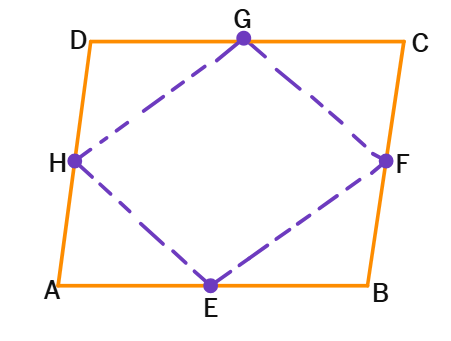
Solution:
Given:
ABCD is a quadrilateral.
E, F, G, H are midpoints of AB, BC, CD, DA respectively.
To Prove:
EFGH is a parallelogram.
Proof:
Join AC.
In ΔABC, E and F are midpoints of
By midpoint theorem, EF || AC and EF =
In ΔADC, G and H are midpoints of CD and
By midpoint theorem, GH || AC and GH =
Therefore, EF || GH and EF =
A quadrilateral with one pair of opposite sides equal and parallel is a
Therefore, EFGH is a parallelogram.
3. Show that the figure formed by joining the midpoints of sides of a rhombus successively is a rectangle.
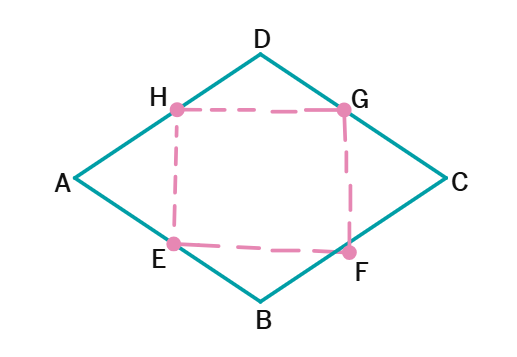
Solution:
Given:
ABCD is a rhombus.
P, Q, R, S are midpoints of AB, BC, CD, DA respectively.
To Prove:
PQRS is a rectangle.
Proof:
Join AC and BD.
By midpoint theorem, PQ ||
Similarly, PS ||
Since AC ⊥ BD, PQ ⊥ PS, QR ⊥ RS. (Diagonals of rhombus are perpendicular)
Therefore, ∠P = ∠Q = ∠R = ∠S =
A parallelogram with all angles 90° is a
Therefore, PQRS is a rectangle.
4. In a parallelogram ABCD, E and F are the midpoints of the sides AB and DC respectively. Show that the line segments AF and EC trisect the diagonal BD.
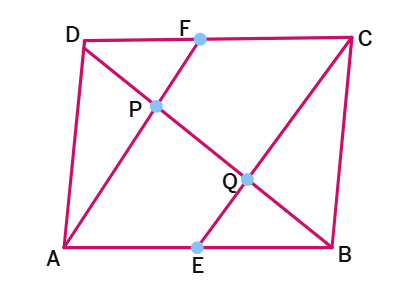
Solution:
Given:
ABCD is a parallelogram.
E and F are midpoints of AB and [DC] respectively.
To Prove:
AF and EC trisect diagonal BD.
Proof:
AB || CD and AB =
Since E and F are midpoints, AE =
Therefore, AE =
AECF is a parallelogram.
AF ||
In ΔDQC, F is the midpoint of
By converse of midpoint theorem, P is midpoint of
DP =
In ΔAPB, E is the midpoint of AB and EQ || AP.
By converse of midpoint theorem, Q is midpoint of
BQ =
DP = PQ = QB.
Therefore AF and EC trisect BD.
5. Show that the line segments joining the midpoints of the opposite sides of a quadrilateral and bisect each other.
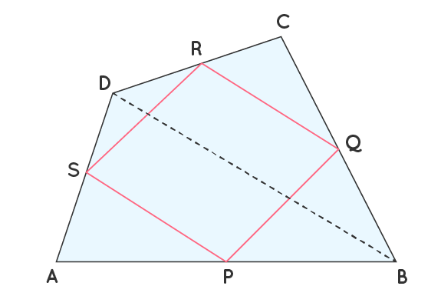
Solution:
Given:
ABCD is a quadrilateral.
E, F, G, H are midpoints of AB, BC, CD, DA respectively.
To Prove:
EG and FH bisect each other.
Proof:
Join AC and BD.
By midpoint theorem, EF ||
EF || GH and EF = GH =
EFGH is a
Diagonals of a parallelogram bisect each other.
Therefore, EG and FH bisect each other.
6. ABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and Parallel to BC intersects AC at D. Show that:
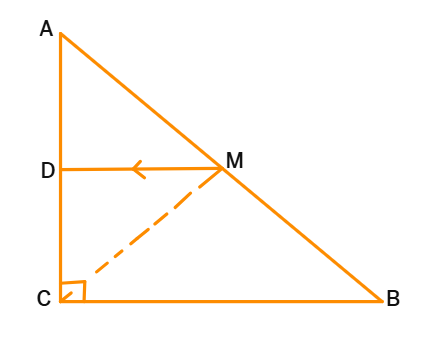
(i) D is the midpoint of AC
(ii) MD ⊥ AC
(iii) CM = MA = 1/2 AB.
VIII. Move T1 leftwards by a distance of H1
Sol 3
1. Which of the following is true about ∆ABC and ∆ADC? These triangles are formed by cutting the parallelogram ABCD along the diagonal AC.
(a) They are congruent to each other.
Yes, the triangles ∆ABC and ∆ADC are congruent because they share the same side (AC), and their corresponding angles are equal due to the properties of a parallelogram.
(b) Both of them have a common hypotenuse, which is AC. This statement is incorrect. AC is not a hypotenuse because these are not right-angled triangles. AC is the diagonal of the parallelogram, not the hypotenuse.
(c) They lie between the same parallels and have equal base lengths.
Yes, both triangles lie between the same parallel lines (AB and CD) and have equal base lengths (AB and CD are equal in a parallelogram).
(d) The area of each of them is half of the area of the parallelogram ABCD.
Yes, the diagonal divides the parallelogram into two equal-area triangles. So the area of each triangle is half of the area of the parallelogram. Correct options: (a), (c), (d)
2. Will the triangles ABC and ADC overlap exactly when folded along AC?
Yes, when you fold the parallelogram along the diagonal AC, the triangles ∆ABC and ∆ADC will overlap exactly because they are congruent.
3. Which of the following quadrilaterals will result in complete overlap of the triangles when folded along the diagonals?
(a) Square Yes, folding along a diagonal of a square results in two congruent triangles that overlap exactly.
(b) Rectangle Yes, folding along a diagonal of a rectangle results in two congruent triangles that overlap exactly.
(c) Rhombus Yes, folding along a diagonal of a rhombus also results in two congruent triangles that overlap exactly.
(d) Trapezium No, folding a trapezium along a diagonal will not result in two congruent triangles unless it is an isosceles trapezium. Correct options: (a), (b), (c)
4 Steps for Shubhajit to cover T2 with T1 (in correct order): IV. Rotate T1 by 180°, clockwise/anti-clockwise, about the top-left corner of the parallelogram.
This is the first step to orient T1 for alignment with T2. V. Move T1 downward by a distance of H2.
After rotation, T1 needs to be moved downwards by the distance between the shorter sides (H2). VIII. Move T1 leftwards by a distance of H1.
Finally, move T1 leftwards by the distance between the longer sides (H1) to align it over T2. So, the correct steps in order are: IV → V → VIII
