Exercise 8.3

1. The opposite angles of a parallelogram are (3x - 2)° and (x + 48)°. Find the measure of each angle of the parallelogram.

Solution:

Key Property: Opposite angles of a parallelogram are equalnot equal.

Therefore, we can set up an equation:

3x - 2 = x + 48

Solving for x:

x =

x =

Now, substitute the value of x back into the expressions for the angles:

Angle 1: (3x - 2)° = (3 × - 2)° = 73°75°

Angle 2: (x + 48)° = (25 + 48)° = 73°75°

Since opposite angles are , the other two angles of the parallelogram also measure 73°75°.

Therefore, each angle of the parallelogram measures 73°.

2. Find the measure of all the angles of a parallelogram if one angle is 24° less than twice the smallest angle.

Solution:

2. Find the measure of all the angles of a parallelogram if one angle is 24° less than twice the smallest angle.

Solution:

Let the smallest angle of the parallelogram be x.

According to the problem, one angle is 24° less than twice the smallest angle, so we express it as:

Larger angle = 2x -

Step 1: Use the sum of angles property

The sum of the interior angles of a parallelogram is always 360°180°, and opposite angles are .

Thus, we can write:

x + (2x - 242x + 24) + x + (2x - 24x - 24) = 360

Step 2: Solve for x

- = 360

x =

x =

Step 3: Find the larger angle

2() - 24 = - 24 =

Step 4: Verify the angles

The two smaller angles are 68°112° each.

The two larger angles are 112°68° each.

Sum: 68 + 112 + 68 + 112 = 360°180°

3. In the adjacent figure ABCD is a parallelogram and E is the midpoint of the side BC. If DE and AB are produced to meet at F, show that AF = 2AB.

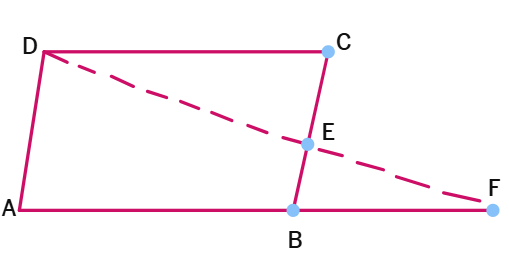
Solution:

Given:

ABCD is a parallelogram.

E is the midpoint of .

DE and AB are produced to meet at .

To Prove:

AF = 2AB

Proof:

In ΔDEC and ΔFEB:

∠DEC = (Vertically opposite angles)

∠DCE = (Alternate interior angles, since DC || AB)

CE = (E is the midpoint of BC)

By congruence rule, ΔDEC ≅ ΔFEB.

Therefore, DC = (CPCTC).

Since ABCD is a parallelogram, AB = (Opposite sides of a parallelogram are equal).

So, AB = .

AF = AB + .

Substitute FB = AB,

AF = AB + .

AF = .

4. In the adjacent figure ABCD is a parallelogram P and Q are the midpoints of sides AB and DC respectively. Show that PBCQ is also a parallelogram.

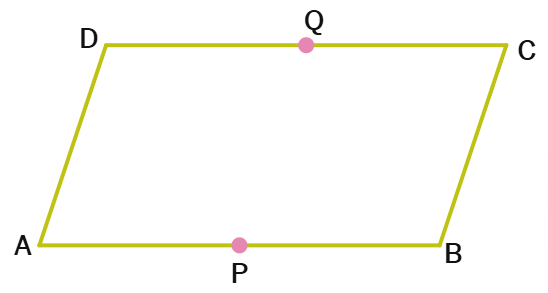
Solution:

Given:

ABCD is a parallelogram.

P is the midpoint of .

Q is the midpoint of .

To Prove:

PBCQ is a parallelogram.

Proof:

Since ABCD is a parallelogram, AB = and AB || .

Since P and Q are midpoints, AP = PB = 12ABAB and DQ = QC = 12DCDC.

Since AB = DC, PB = .

Also, since AB || DC, PB || QC.

A quadrilateral with one pair of opposite sides equal and parallel is a parallelogramrhombus.

Therefore, PBCQ is a parallelogram.

5. ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle QAC and CD || BA as shown in the figure. Show that:

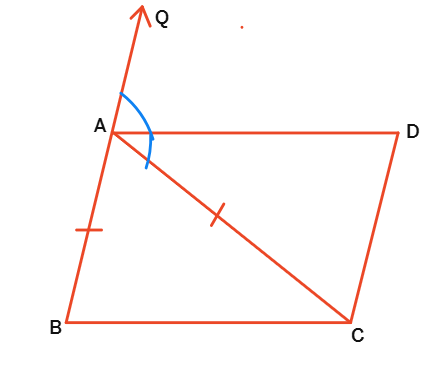
(i) ∠DAC = ∠BCA

(ii) ABCD is a parallelogram.

Solution:

Given:

ABC is an isosceles triangle with AB = .

AD bisects exterior angle .

CD || .

Proof:

(i) ∠DAC = ∠BCA

Since AB = AC, ∠ABC = ∠BCA∠BAC (Angles opposite to equal sides are equal).

∠QAC = ∠ABC + ∠BCA∠BAC (Exterior angle property).

∠QAC = ∠BCA (Since ∠ABC = ∠BCA).

AD bisects ∠QAC, so ∠DAC = 1/2∠QAC∠QAC.

∠DAC = 1/2 (2∠BCA) = ∠BCA.

(ii) ABCD is a parallelogram

CD || (Given).

∠DAC = ∠BCA (Proved).

∠BAC = ∠BCA∠CBA (Since AB = AC).

∠DAC = ∠BAC∠BCA.

∠DAC = ∠CDA (Alternate interior angles, since CD || BA).

∠BAC = ∠CDA∠CBA.

AB || CD and AC || BD (Since ∠BAC = ∠CDA).

A quadrilateral with both pairs of opposite sides parallel is a parallelogramrectangle.

Therefore, ABCD is a parallelogram.

6. ABCD is a parallelogram AP and CQ are perpendiculars drawn from vertices A and C on diagonal BD (see figure) show that

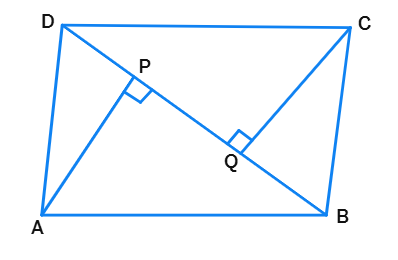
(i) ΔAPB ≅ ΔCQD

(ii) AP = CQ.

Solution:

Given:

ABCD is a parallelogram.

AP ⊥ .

CQ ⊥ .

Proof:

(i) ΔAPB ≅ ΔCQD

In ΔAPB and ΔCQD:

∠APB = ∠CQD = 90°180° (Given)

AB = (Opposite sides of a parallelogram are equal)

∠ABP = ∠CDQ∠CQD(Alternate interior angles, since AB || CD)

By AAS congruence rule, ΔAPB ≅ ΔCQD.

(ii) AP = CQ

Since ΔAPB ≅ ΔCQD (Proved), AP = (CPCTC).

7. In Δs ABC and DEF, AB || DE; BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see figure). Show that:

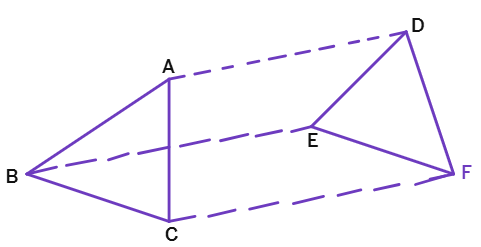
(i) ABED is a parallelogram

(ii) BCFE is a parallelogram

(iii) AC = DF

(iv) ΔABC ≅ ΔDEF.

Solution:

Given:

AB ||

BC =

BC ||

Proof:

(i). ABED is a parallelogram:

AB || DE (Given)

BE = (Since ABED is formed by joining vertices)

A quadrilateral with one pair of opposite sides parallel and equal is a parallelogramrhombus.

Therefore, ABED is a parallelogram.

(ii). BCFE is a parallelogram:

BC || (Given)

BC = (Given)

A quadrilateral with one pair of opposite sides parallel and equal is a .

Therefore, BCFE is a parallelogram.

(iii). AC = DF:

ABED is a parallelogram (Proved), so AD = .

BCFE is a parallelogram (Proved), so CF = .

Therefore, AD = .

In ΔABC and ΔDEF:

AB = (Opposite sides of parallelogram ABED)

BC = (Given)

∠ABC = ∠DEF∠DFE (Corresponding angles, since AB || DE and BC || EF)

By SASSSSASA congruence rule, ΔABC ≅ ΔDEF.

Therefore, AC = (CPCTC).

(iv). ΔABC ≅ ΔDEF:

AB = (Opposite sides of parallelogram ABED)

BC = (Given)

AC = (Proved)

By SSSSASASA congruence rule, ΔABC ≅ ΔDEF.

8. ABCD is a parallelogram. AC and BD are the diagonals intersect at O. P and Q are the points of tri section of the diagonal BD. Prove that CQ || AP and also AC bisects PQ (see figure).

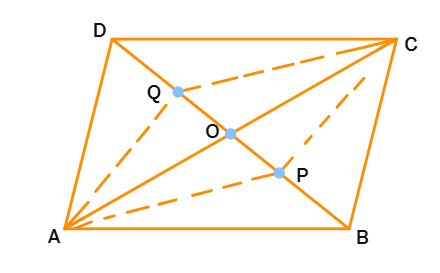
Solution:

Given:

ABCD is a parallelogram.

AC and BD are diagonals intersecting at .

P and Q are points of trisection of .

To Prove:

CQ || AP

AC bisects PQ

Proof:

Since ABCD is a parallelogram, O is the midpoint of BD.

Since P and Q trisect BD, BP = PQ = .

Therefore, OP = .

In ΔAOQ and ΔCOP:

AO = (Diagonals of parallelogram bisect each other)

∠AOQ = ∠COP∠CPO (Vertically opposite angles)

OP = (Proved above)

By SASSSSASA congruence rule, ΔAOQ ≅ ΔCOP.

Therefore, ∠OAQ = ∠OCP∠OPC (CPCTC).

Since ∠OAQ = ∠OCP, AP || (Alternate interior angles are equal).

Let AC intersect PQ at M.

In ΔOMQ and ΔOMP:

= OP (Proved above)

∠MOQ = ∠MOP∠MPO (Vertically opposite angles)

OM = OM (Common side)

By SASSSSASA congruence rule, ΔOMQ ≅ ΔOMP.

Therefore, PM = (CPCTC).

Hence, AC bisects PQ.

9. ABCD is a square. E, F, G and H are the mid points of AB, BC, CD and DA respectively. Such that AE=BF=CG=DH. Prove that EFGH is a square.

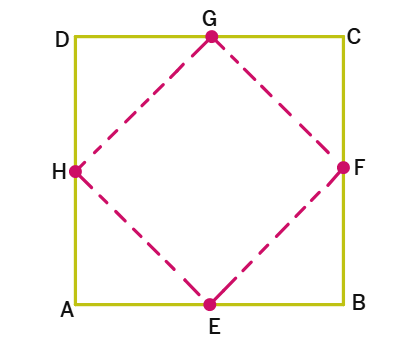
Solution:

Given:

ABCD is a square.

E, F, G, H are midpoints of AB, BC, CD, DA respectively.

AE = BF = CG = DH.

To Prove EFGH is a square:

Proof:

Since E, F, G, H are midpoints, AE = EBAB = BF = FC = CGCD = GD = DHHA = HA.

In ΔAEH and ΔBFE:

AE = BF (Given)

AH = (Since ABCD is a square and midpoints)

∠A = ∠B = 90°180° (Angles of a square)

By SASSSSASA congruence rule, ΔAEH ≅ ΔBFE.

Therefore, EH = (CPCTC).

Similarly, we can prove EF = FG = GH = HE.

Thus, EFGH is a rhombusparalellogram.

In ΔAEH, ∠AEH + ∠AHE = 90°180° (Since ∠A = 90°).

In ΔBFE, ∠BFE + ∠BEF = 90°180° (Since ∠B = 90°).

Since ΔAEH ≅ ΔBFE, ∠AEH = ∠BFE∠BEF and ∠AHE = ∠BEF∠BFE.

∠HEF = 180° - (∠AEH + ∠BEF) = 180° - (∠AEH + ∠AHE) = 180° - 90°180° = 90°180°.

Similarly, ∠EFG = ∠FGH = ∠GHE = 90°180°.

Since EFGH is a rhombus with all angles 90°, EFGH is a squarerectangle.