Parallelogram and their Properties
A quadrilateral has four sides, four angles and four vertices.
A

Activity: Make a random parallelogram from a sheet of paper. Draw one of its diagonals and cut along it. We now have two triangles. What can be said about both these triangles?
Try placing one triangle over the other. As it turns out, both the two triangles are congruent to each other. Try doing it a few more times with different parallelograms.
Now, let's prove this result.
Theorem: A diagonal of a parallelogram divides it into two congruent triangles.
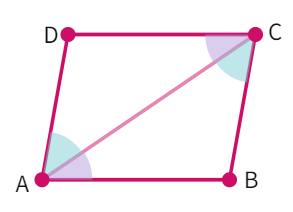
Proof: Let ABCD be a parallelogram and AC be a diagonal. The diagonal AC divides parallelogram ABCD into two triangles, namely, ∆ ABC and ∆ CDA.
- From the figure, we know: BC || AD and AC is a
. - We see: ∠ BCA = ∠
(Pair of alternate angles). - Similarly, AB || DC and AC is a transversal.
- ∠ BAC = ∠
(Pair of alternate angles) - AC =
as they are a common side. - ∆ ABC ≅ ∆
by congruency rule. - Diagonal AC divides parallelogram ABCD into two congruent triangles ABC and CDA
Theorem : If a quadrilateral is a parallelogram, then each pair of its opposite sides is equal.

- We already know that ∆ ABC ≅ ∆
by congruency rule. - Since, the corresponding parts of congruent triangles are also equal: AB =
and = BC - Thus, opposite sides of a parallelogram are equal.
Theorem : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
- Taking a quadrilateral where AB =
and AD = - With the diagonal AC drawn, we get ∆ABC and ∆CDA where:
- AD = BC and CD = AB are given
- AC =
as it is a side - Thus, ∆ ABC ≅ ∆
by congruency rule. - From CPCT, we get: ∠ BAC = ∠
and ∠ BCA = ∠ - These are alternate interior angles for the quadrilateral ABCD.
- Since, alternate interior angles are equal- quadrilateral ABCD is a parallelogram.
Therefore, in a parallelogram each pair of opposite sides is equal and conversely if each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Theorem : In a parallelogram, opposite angles are equal

- We know that when the diagonal of a parallelogram is drawn, we get two congruent triangles.
- With the diagonal AC drawn, we get ∆ ABC ≅ ∆
- Thus from CPCT, we get: ∠ ABC = ∠
which (as seen) are opposite angles. - Similarly, if we draw diagonal BD, we get ∆ BCD ≅ ∆
- From CPCT, we get: ∠BCD = ∠
- These are opposite angles of a parallelogram.
- Thus, the opposite angles of a parallelogram are equal.
Now, is the converse true ?
Theorem : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
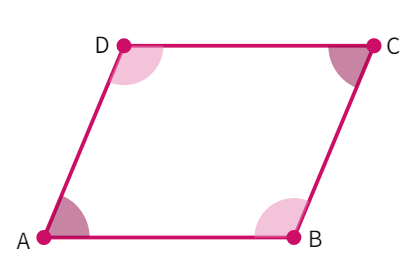
- We have quadrilateral ABCD with ∠ABC = ∠ADC and ∠DAB = ∠BCD.
- We also know: ∠ABC + ∠ADC + ∠DAB + ∠BCD =
° (angle sum property) - Combining the angle sum with the fact that opposite angles are equal we get: ∠ABC + ∠
= ° - In a pair of parallel lines being cut through with a transverse, the co-interior angles are
. - Thus, we can say: AD ∥
with as transverse - Similarly, we get ∠ABC + ∠
= ° - Which again, gives us: AB ∥
with as transverse. - Since, both the opposite sides are
, quadrilateral ABCD is a .
Example 1 : Show that each angle of a rectangle is a right angle.

