Exercise 8.1
1. State whether the statements are True or False.
Solution:
(i) Every parallelogram is a trapezium (
(ii) All parallelograms are quadrilaterals (
(iii) All trapeziums are parallelograms (
(iv) A square is a rhombus (
(v) Every rhombus is a square (
(vi) All parallelograms are rectangles (
2. Complete the following table by writing (YES) if the property holds for the particular Quadrilateral and (NO) if property does not hold.
Solution:
| Properties | Trapezium | Parallelogram | Rhombus | Rectangle | Square |
|---|---|---|---|---|---|
| a. Only one pair of opposite sides are parallel | YES | ||||
| b. Two pairs of opposite sides are parallel | |||||
| c. Opposite sides are equal | |||||
| d. Opposite angles are equal | |||||
| e. Consecutive angles are supplementary | |||||
| f. Diagonals bisect each other | |||||
| g. Diagonals are equal | |||||
| h. All sides are equal | |||||
| i. Each angle is a right angle | |||||
| j. Diagonals are perpendicular to each other |
3. ABCD is trapezium in which AB || CD. If AD = BC, show that ∠A = ∠B and ∠C = ∠D.
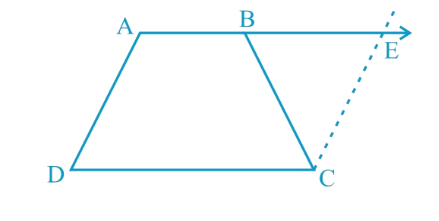
Solution:
Given:
ABCD is a trapezium where AB ||
AD =
To prove that ∠A = ∠B and ∠C = ∠D in a trapezium ABCD where AB || CD and AD = BC:
Construction:
Extend AB and draw a line through C parallel to DA, intersecting AB produced at E.
Proof:
Since AD || CE and AE || CD, AECD is a parallelogram.
Therefore, AD = EC.
Given that AD = BC, it follows that BC = EC.
In triangle BCE, since BC = EC, the angles opposite these equal sides are also equal, so ∠CBE = ∠CEB.
Because AECD is a parallelogram, ∠A + ∠E = 180° (sum of adjacent angles in a parallelogram).
Also, ∠B + ∠CBE = 180° (linear pair).
Substituting ∠CEB for ∠CBE, ∠A + ∠CEB = 180°.
Comparing the two equations, ∠A = ∠B.
Since AB || CD, ∠A + ∠D = 180° and ∠B + ∠C = 180°.
Because ∠A = ∠B, it follows that ∠C = ∠D.
Therefore, it has been proven that in trapezium ABCD, if AB || CD and AD = BC, then ∠A = ∠B and ∠C = ∠D.
∠C = ∠D
Since AECD is a parallelogram, ∠D = ∠AEC (Opposite angles of a parallelogram are equal).\
In ΔBCE, ∠C + ∠BEC + ∠B = 180° (Angle sum property).
Substituting ∠AEC for ∠D and ∠B for ∠BEC, we get ∠C + ∠AEC + ∠B = 180°.
Since AB || CE and BC is a transversal, ∠C + ∠B = 180° (Co-interior angles).
Comparing equations, we get ∠C + ∠AEC + ∠B = ∠C + ∠B.
Therefore, ∠AEC = 0°, which is not possible. Hence, our assumption that AECD is a parallelogram is incorrect.
This implies that CE and AD are not parallel. Therefore, ∠D and ∠AEC are not equal.
However, since AB || CD and BC is a transversal, ∠C + ∠B = 180° (Co-interior angles).
And since AB || CD and AD is a transversal, ∠A + ∠D = 180° (Co-interior angles).
Comparing equations, and using the fact that ∠A = ∠B, we get ∠C + ∠B = ∠A + ∠D = ∠B + ∠D.
Therefore, ∠C = ∠D.
4. The four angles of a quadrilateral are in the ratio 1![]() 3:4. Find the measure of each angle of the quadrilateral.
3:4. Find the measure of each angle of the quadrilateral.
Solution:
Let the angles of the quadrilateral be x, 2x, 3x, and 4x.
The sum of the angles of a quadrilateral is 360°.
Therefore, x + 2x + 3x + 4x =
x =
So, the angles of the quadrilateral are:
x = 36°
2x = 2 × 36° =
3x = 3 × 36° =
4x = 4 × 36° =
Therefore, the measures of the angles of the quadrilateral are 36°, 72°, 108°, and 144°.
5. ABCD is a rectangle AC is diagonal. Find the nature of ΔACD. Give reasons.
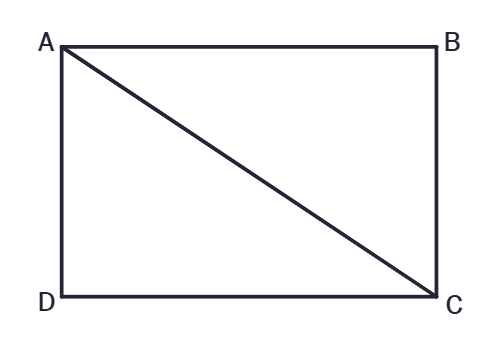
Solution:
Given:
ABCD is a rectangle.
AC is a diagonal.
To Find the nature of ΔACD:
Reasons:
ABCD is a rectangle: This means all angles are
Properties of a rectangle: Opposite sides are
Consider ΔACD:
∠ADC =
Nature of ΔACD:
ΔACD is a
Conclusion:
ΔACD is a right-angled triangle.
