Exercise 8.2
1. In the adjacent figure ABCD is a parallelogram ABEF is a rectangle show that ΔAFD ≅ ΔBEC.
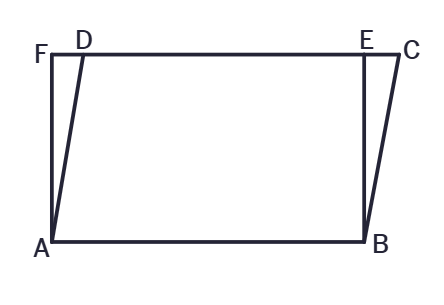
Solution:
Given:
ABCD is a
ABEF is a
To Prove:
ΔAFD ≅ ΔBEC
Proof:
In parallelogram ABCD:
AD =
In rectangle ABEF:
AF =
Since ABEF is a rectangle, ∠FAB = ∠EBA =
∠FAB + ∠FAD =
∠FAD =
Similarly, ∠EBC = 90°
Therefore:
∠FAD = ∠EBC =
Now, consider ΔAFD and ΔBEC:
AD =
AF =
∠FAD =
By
ΔAFD ≅
Conclusion:
Therefore, ΔAFD ≅ ΔBEC.
2. Show that the diagonals of a rhombus divide it into four congruent triangles.
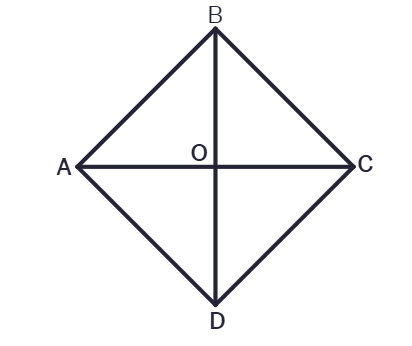
Solution:
Given:
ABCD is a rhombus.
To Prove:
The diagonals of rhombus ABCD divide it into four congruent triangles.
Proof:
Properties of a rhombus:
All sides are equal: AB = BC = CD = DA
Diagonals bisect each other at right angles.
Let the diagonals AC and BD intersect at point O.
AO =
BO =
∠AOB = ∠BOC = ∠COD = ∠DOA =
Consider the four triangles formed: ΔAOB, ΔBOC, ΔCOD, and ΔDOA.
In ΔAOB and ΔBOC:
AO =
BO = BO (Common side)
∠AOB = ∠BOC =
By
Similarly, we can prove:
ΔBOC ≅ ΔCOD
ΔCOD ≅ ΔDOA
ΔDOA ≅ ΔAOB
Therefore, all four triangles are
ΔAOB ≅ ΔBOC ≅ ΔCOD ≅ ΔDOA
Conclusion:
The diagonals of a rhombus divide it into four congruent triangles.
3. In a quadrilateral ABCD, the bisectors of ∠C and ∠D intersect at O. Prove that ∠COD = 1/2(∠A + ∠B).
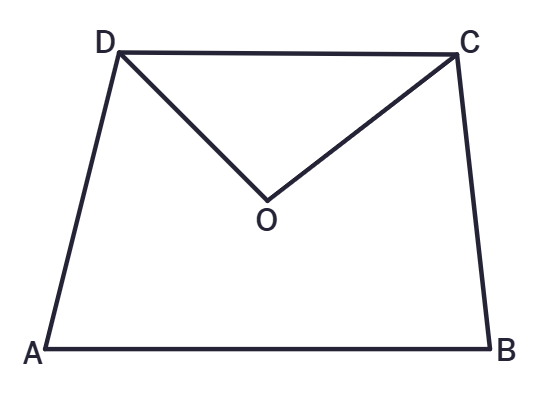
Solution:
Given:
ABCD is a quadrilateral.
CO is the bisector of
DO is the bisector of
To Prove:
∠COD = 1/2(∠A + ∠B)
Proof:
In quadrilateral ABCD, the sum of all angles is
∠A + ∠B + ∠C + ∠D = 360°
Since CO and DO are bisectors of ∠C and ∠D, respectively:
∠CDO =
∠DCO =
In triangle COD, the sum of all angles is
∠COD +
Substitute ∠CDO and ∠DCO from above:
∠COD +
Multiply the equation by 2:
From above, we know ∠A + ∠B + ∠C + ∠D = 360°. Equate this with the previous equation:
2∠COD + ∠D + ∠C = ∠A + ∠B + ∠C + ∠D
Subtract ∠C and ∠D from both sides:
2∠COD =
Divide both sides by 2:
∠COD =
Conclusion:
Therefore, ∠COD = 1/2(∠A + ∠B).
