Enhanced Curriculum Support
This is a comprehensive educational resource designed to provide students with the tools and guidance necessary to excel. This support system is structured to cater to various aspects of learning, ensuring that students are well-prepared for academic challenges and practical applications of mathematical concepts. Some are the key benefits are mentioned below:
Comprehensive Learning: This holistic approach helps students gain a thorough understanding of the subject. Practical Application: The resources encourage students to apply mathematical concepts to real-life scenarios, enhancing their practical understanding and problem-solving skills.
Exam Preparedness: Sample Question Papers provide ample practice for exams. They help students familiarize themselves with the exam format and types of questions, reducing exam anxiety.
Sec A
(1) If n(A) = 10, n(B) = 6 and n(A ∪ B) = 12, then n(A ∩ B) = ................
(2) The roster form of the set A = { x : x =
(A) A = {1, 4, 9, 16, 25}
(B) A = {0, 1, 4, 9, 16}
(C) A = {1, 4, 9, 16}
(D) A = {0, 1, 4, 9, 16, 25}
(3) Set A = {x : x is a letter in the word "CHANDRAYAN"}, then n(A) is ......
(A) 10
(B) 7
(C) 8
(D) 6
(4) The number of subsets of a set is 16, then the number of elements of the set is ......
(A) 8 (B) 16 (C) 10 (D) 4
(5) If A = {x : x is a factor of 24}, then find n(A).
(6) Give one example each for a finite set and an infinite set.
(7) If A = {x : x is a factor of 24}, then find n(A).
Sec B
(1) Express the following sets in set-builder form :
(i) A = {1, 8, 27, 64}
(ii) B = {-3, -2, -1, 0, 1, 2}
(2) If μ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {2, 3, 5, 8} and B = {0, 3, 5, 7, 10}. Then represent A ∩ B in the Venn diagram.
Sec C
1. If A = {x : 2x + 1, x ∈ N, x ≤ 5}, B = {x : x is a composite number, x ≤ 12}, then show that (A ∪ B) - (A ∩ B) = (A - B) ∪ (B - A).
2. If A = {x : x is a factor of 6}, B = {x : x is a positive even number less than 10}, then find (i) A ∪ B, (ii) A ∩ B, (iii) A - B by Venn diagram.
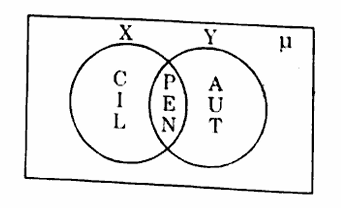
(3) From the Venn diagram, find the following sets.
(i) X ∪ Y (ii) X ∩ Y (iii) X - Y (iv) Y - X
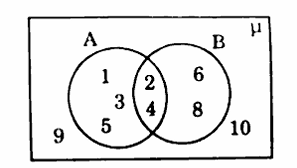
(4) From the given Venn diagram show that n(A ∪ B) = n(A) + n(B) - n(A ∩ B).
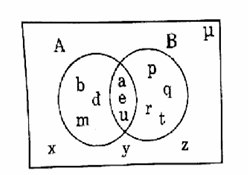
(5) From the given Venn diagram, find the sets A ∪ B, A ∩ B, A – B and B – A.
(6) A = {x : x is a perfect square, x < 50, x ∈ N}
B = {x : x = 8m + 1, where m ∈ W, x < 50, x ∈ N}
Find A ∩ B and display it with Venn diagram.
(7) If A = {1, 2, 3, 4, 5} and B = {2, 4, 6, 8}, then show that n(A ∪ B) = n(A) + n(B) - n(A ∩ B).
Sec D
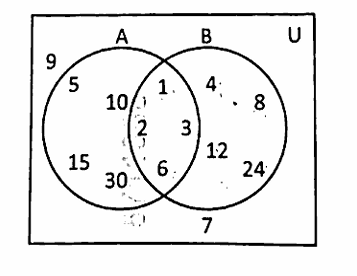
(1) From the given Venn diagram, write the sets A ∪ B, A ∩ B, A - B and B - A.