Universal Set And Subset
A universal set (U) is a collection that contains all elements under discussion. Any specific group or category within this universal set is called a subset.
Example: Teeth Classification
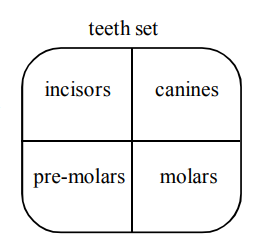
Consider the set of teeth divided into four groups:
- Incisors
- Canines
- Premolars
- Molars
Here, the whole set of teeth is the universal set, and the four groups are its subsets.
Every tooth type belongs to the universal set, meaning molars, premolars, incisors, and canines are all part of the universal set of teeth.
The universal set is generally denoted by 'μ' or 'U' and is often represented using a
A subset is a set where every element belongs to a larger set.
We denote a subset as A ⊆ B, meaning every element of A is also in B.
Example: Natural Numbers and Their Subsets Consider the set of natural numbers: N = {1, 2, 3, 4, 5, ...}
Some subsets of N:
Even numbers: E = {2, 4, 6, 8, ...}
Odd numbers: O = {1, 3, 5, 7, ...}
Since every element in E and O is already in N, we can say: E ⊆ N** and O ⊆ N
Example: Smaller Sets Within a Given Set Consider the set A = {1, 2, 3}.
The possible subsets are: {1}, {2}, {3} , {1,2}, {1,3}, {2,3} , {1,2,3}
Thus, the total number of subsets of a set with n elements is 2ⁿ.
Example: Classification of Number Sets
N = {1, 2, 3, 4, ...} (Natural numbers)
W = {0, 1, 2, 3, ...} (Whole numbers)
Z = {..., -2, -1, 0, 1, 2, ...} (Integers)
Q = Rational numbers (fractions like
1 2 3 4 R = Real numbers (including irrational numbers like
2
Since each of these sets builds upon the previous one, we can express their relationships as: N ⊆ W ⊆ Z ⊆ Q ⊆ R
1. Null Set (Ø)
A null set (or empty set) has no elements.
It is a subset of every set.
Example: The set of
2. Every Set is a Subset of Itself
- A set A is always a subset of itself: A
3. Proper Subset
- A proper subset of a set B contains some, but not all, elements of B.
- Example: V = {a, e, i, o, u} is a subset of the alphabet set A = {a, b, c, ..., z}, but it
So, V ⊂ A.
